It can be assumed that the
civilizations present in the galaxy will be distributed
over the entire historical development evels. In a first
approach one could assume that all civilizations are
equally distributed over the levels of civilization.
On the other hand, it can be argued that the longer a
civilization exists, the greater the probability of an
all-destroying catastrophe. It is therefore more probable
that the number of civilizations will decrease as the
level of development increases. The following approach
can be formulated from this:
| 6.2.1
Approach |
The probability Fz for a
civilization is inversely proportional to the
level of development.
Fz = 1:m and m
= development level |
This is illustrated once again in the following graphic.
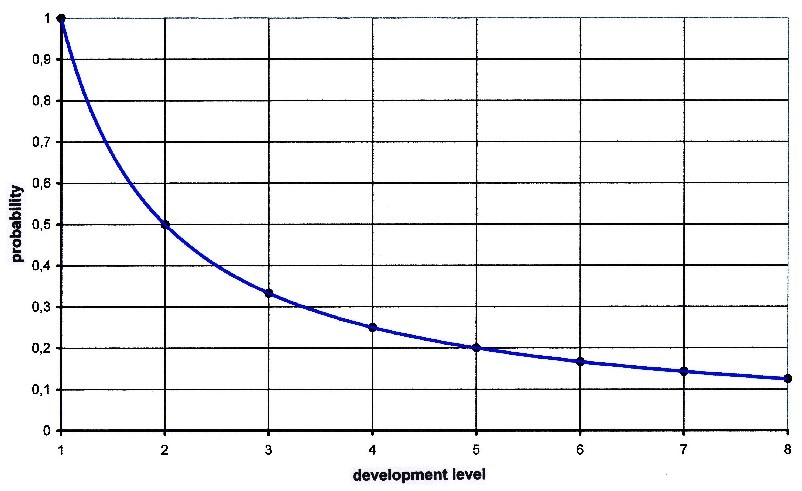
If intelligent life has been created on a planet, it is
100% likely that preliminary levels of civilizations have
also been created, exactly those of level 1.
But already at level 2 the probability is only 0.5, at
level 3 still 0.33, at level 4 only 0.25 etc.
It must now be demanded that the sum of all probabilities
for the levels of civilization (m > 2) is equal to
one. This means that it is 100% probable that at least
one exists at the sum of all levels of civilization.
So the rule is:
| 6.2.2
Equation |
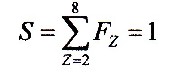 |
However, this is not the case with
the previous approach 6.2.1, because totalling provides:
S = 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 +
1/8 = 481 : 280 > 1
However, probabilities cannot become greater than one. We
must therefore take a tougher approach.
A better approach can be achieved by using the square of
the development level to calculate the probability Fz
Fz
= 1:m2 and m
> 1 is development level
The totals are provided here:
S = 1/4 + 1/9 + 1/16 + 1/25 + 1/36 + 1/49 + 1/64
S = 7.301 : 14.400
S = 0.507,013
Then the normalization function 6.2.2 can be modified in
this way:
| 6.2.3
Equation |
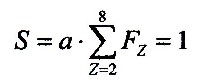 |
In order to adjust the developmental step function, the
factor a must be equal to the reciprocal of the sum,
thus:
a = 14,400 :
7,301
a = 1.972,332
Thus, the following approach can
now be established for the probability of a development
level:
| 6.2.4
Equation |
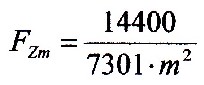 |
m >
1 |
The following graphic shows this once more.
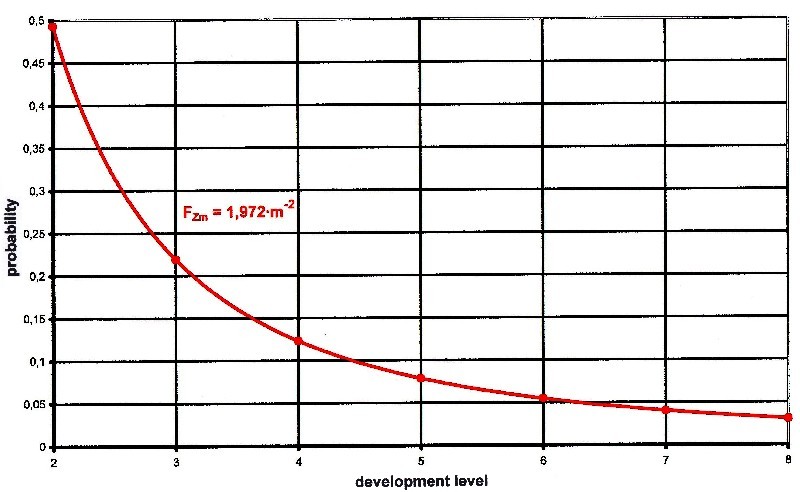
The development level function 6.2.4 can still determine
the total probability for all civilization levels greater
than 2.
The total probability is represented by the area spanned
under the function. So you have to form the integral
above the function. This can then be formulated as
follows:
The total probability for the existence of a civilization
corresponds to the integral over the probability function
of a civilization.
| 6.2.5
Equation |
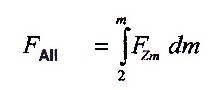 |
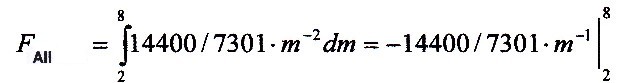
FAll = 14400/7301 ·
(-8-1 + 2-1)
Fall = 5400/7301 = 0.739,624
This means that there is a total probability of
encountering a civilization at all of about 74%.
With the probability function for civilization levels, an
effective tool is now available to describe and classify
the probabilities for the development levels of a
civilization. Now only one thing has to be taken for
granted:
| 6.2.6 Axiom |
All considerations on levels
of development, development time, and the
distribution of levels of civilization are
transferable to extraterrestrial civilizations. |
|